 M (an observation point)
M (an observation point)
Consider two independent finite samples {x1i}
i=1k and {x
2i}
i=1k of size k from
distributions F1 and F2 on the unit 2-sphere, S2. We consider following sample
covariances at point q  M (an observation point)
M (an observation point)
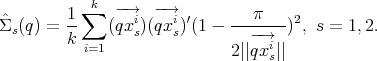
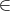
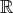 n2×n2 be the mean and covariance of Z = (
n2×n2 be the mean and covariance of Z = (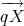 )(
)(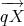 )′, for X ~ F
s.
Thus, we assume that the mean and covarince of the tensor valued trandom
variable Z exist. As an application of the Central Limit Theorem we obtained the
asymptotic
)′, for X ~ F
s.
Thus, we assume that the mean and covarince of the tensor valued trandom
variable Z exist. As an application of the Central Limit Theorem we obtained the
asymptotic
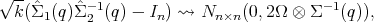
![√-- -1 ′ T -1 ′
ξk(q;h) := k (h(ˆΣ1(q)ˆΣ 2 (q))- h (In )) ⇝ N (0,2[h(In)] (Ω ⊗Σ (q))[h (In)]),](comp_s24x.png) | (1) |
for similarity invariant h which gradient h′(.) 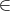
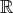 n2 is continuous and does not
vanish at In. For example, ξk(q; tr) =
n2 is continuous and does not
vanish at In. For example, ξk(q; tr) = 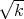 (tr(
(tr(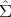 1(q)
1(q)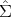 2-1(q)) - n) and
ξk(q; det) =
2-1(q)) - n) and
ξk(q; det) = 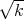 (det(
(det(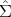 1(q)
1(q)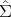 2-1(q)) - 1).
2-1(q)) - 1).
We apply bootstrapping method to utilize (1). For k′ < k, let ym,m = 1,...,M
be instances of statistic ξk(q; h) based on subsamples of size k′ of the initial
k-samples. Then, according to (1), ξ = 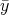 ∕s.e.(y) goes to N(0, 1) in distribution as
k →∞.
∕s.e.(y) goes to N(0, 1) in distribution as
k →∞.
The following applet simulates distributions from different families and calculates ξ statistics. Xi-pval is the p-value of ξ statistics. We choose the observation point q randomly on S2. The user can choose the sample size k and whether the two samples are equally distributed or not, H0 hypothesis. Sub-sample size is fixed to k′ = k∕2 and M = k∕4. Possible choices for function h are the trace, determinant and h(A) = tr(log(A)). Shown are the two k-samples in red and blue and the observation point in green. Drag the mouse over to change the view point.