
Let M be a Riemannian n-manifold with metric tensor G and volume form V ,

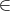 M. If a continuous random
variable on M is given by distribution function in the form
M. If a continuous random
variable on M is given by distribution function in the form
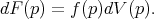
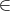 M is defined to be
M is defined to be
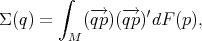
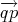 is the tangent vector at q obtained by the inverse exponential map
exp q-1. Σ(q) is a contra-variant 2-tensor on the tangent space M
q. Collectively, Σ
is a tensor field on M, which we call covariance field.
is the tangent vector at q obtained by the inverse exponential map
exp q-1. Σ(q) is a contra-variant 2-tensor on the tangent space M
q. Collectively, Σ
is a tensor field on M, which we call covariance field.
Recall that the metric G is a co-variant tensor field on M. For any q 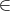 M, the
product G(q)Σ(q) is a linear operator on the tangent space Mq, which trace
is
M, the
product G(q)Σ(q) is a linear operator on the tangent space Mq, which trace
is
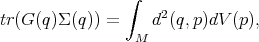
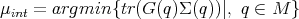
Given a distribution F on M and its covariance operator field GΣ, one can obtain a family of representations of F, by applying a similarity invariant h on it. Similarity invariants are functions that takes as arguments linear operators, such as tr, det and tr2ln, to mention a few. Are such representations true ones? With other words, can one recovers F from h(GΣ)? It turns out that the answer depends on the geometry of M, which is defined by the metric G. The answer is positive when the operators GΣ have no finite rank, or equivalently, the metric G is of full rank. We direct to [4] for more precise exposition of this interesting relationship between geometry and distribution representations.
In canonical coordinates, the metric tensor in the real plane is G(x,y) = I2. The
rank of a k × k matrix of square pairwise distance between k points in the real
plane is always less or equal of 4. As a result, for a distribution in 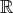 2, if you know
the covariance at one point, you know it for all points. The same is true in higher
dimensions also.
2, if you know
the covariance at one point, you know it for all points. The same is true in higher
dimensions also.
For example, the metric tensor in the hyperbolic plane is G(x,y) = 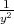 I2 and the
rank of a k × k matrix of squared pairwise distance between k points in the
hyperbolic plane is k (w.p. 1).
I2 and the
rank of a k × k matrix of squared pairwise distance between k points in the
hyperbolic plane is k (w.p. 1).
As we mentioned above, the question of recovering a distribution from its
covariance field is contingent on the properties of the geodesic metric d on M. Let
(U,φ), U ⊂ 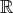 n be a local chart on M. Define ψ(x,y) = d(φ(x),φ(y)), x,y
n be a local chart on M. Define ψ(x,y) = d(φ(x),φ(y)), x,y 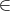 U.
Then we claim that recovering is possible only when ψ does not have a finite
rank.
U.
Then we claim that recovering is possible only when ψ does not have a finite
rank.
For example, if ψ(x,y) = h(< x,y >) for function h that is analytic about the
origin and for which h(s)(0) 0 for infinitely many s, then ψ will not have a finite
rank. By applying this fact for h = cos, we obtain that the rank of the metric on
the unit sphere Sn is not finite and recovering distributions from their covariance
fields is always possible on Sn (w.p.1).
0 for infinitely many s, then ψ will not have a finite
rank. By applying this fact for h = cos, we obtain that the rank of the metric on
the unit sphere Sn is not finite and recovering distributions from their covariance
fields is always possible on Sn (w.p.1).
[1] Balov, N. (2008) Covariance fields, http://arxiv.org/abs/0807.4690v2.
[2] Balov, N. (2008) Covariance of centered distributions on manifold, http://arxiv.org/abs/0805.0732v1.
[3] Balov, N. (2008) Comparing and interpolating distributions on manifold, http://arxiv.org/abs/0807.0782v2.
[4] Balov, N. (2008) On the Stochastic Rank of Metric Functions, http://arxiv.org/abs/0810.5549v2.