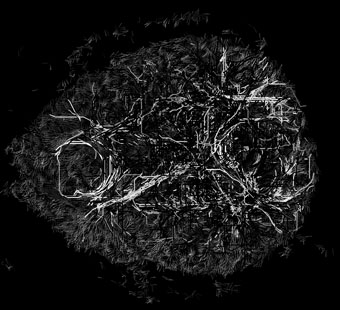
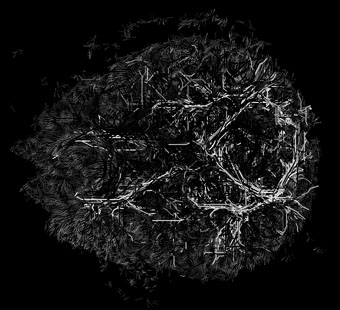
Connectivity Paths in Diffusion-Tensor Images

We extend the dynamic programming algorithm for finding optimal paths in tensor fields by proposing a stochastic solution of a Bayesian problem. Optimality is based on tensor field related cost as well as on geometric properties and prior knowledge. The resulting paths are more resistant to measurement errors and missing data. We demostrate the approach by constructing connectivity paths in DTI volumes.

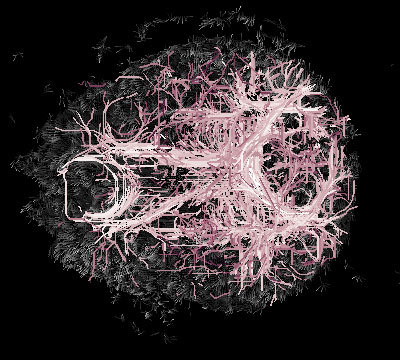
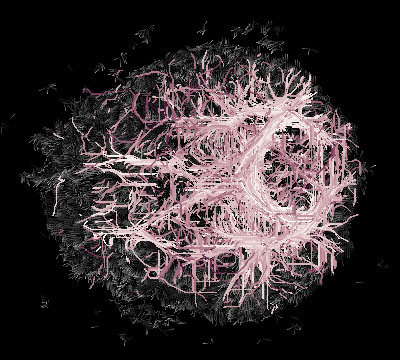
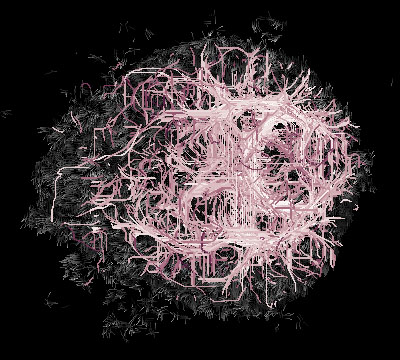
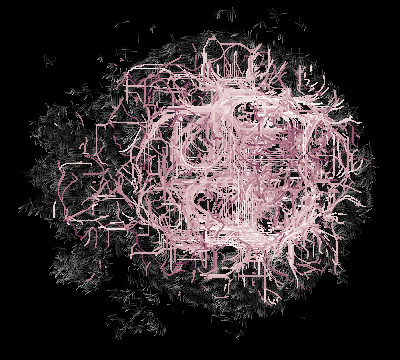
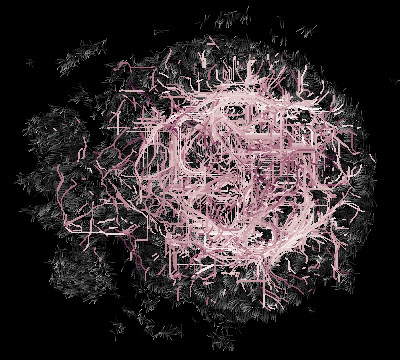
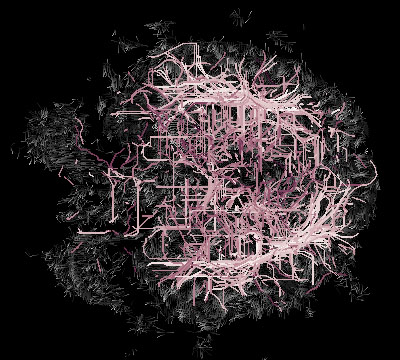
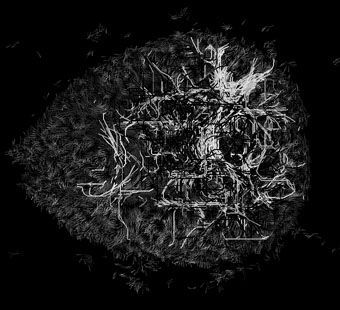
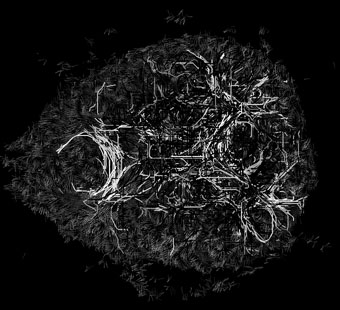
A large sample of optimal paths connecting random pairs of voxels. Paths are intersected with different z-slices.

Locations of visitors to this page
Return home