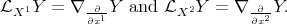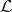 XY we denote the Lie derivative of Y with respect to X. Define the
contra-variant 2-tensor field
XY we denote the Lie derivative of Y with respect to X. Define the
contra-variant 2-tensor field
We demonstrate analysis of vector fields on the sphere using the tensor field of contravariant derivatives. Shown are: a vector field in the top-left corner, the scaler field of vector lengths in top-right, the scalar field of the traces of the contravariant tensor field in botton-left, and the scalar field of the determinants of the contravariant tensor field in the bottom-right.
Let M be a n-manifold and X and Y are two smooth vector fields on M. With
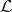 XY we denote the Lie derivative of Y with respect to X. Define the
contra-variant 2-tensor field
XY we denote the Lie derivative of Y with respect to X. Define the
contra-variant 2-tensor field

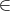 T11(M) is a linear operator field on M. For any similarity invariant h,
h(GW) is a smooth function on M.
T11(M) is a linear operator field on M. For any similarity invariant h,
h(GW) is a smooth function on M.
Let (x1,x2) be parametrizatiom on S2 and let X1 and X2 be the canonical
vector fields 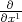 and
and 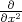 . Then the Lie derivatives with respect to X and Y are in
fact the covariant derivatives
. Then the Lie derivatives with respect to X and Y are in
fact the covariant derivatives