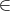 S1, thus f = {f
i}i=1k for f
i = f(pi) On another set of points
{qj}j=1k, q
j
S1, thus f = {f
i}i=1k for f
i = f(pi) On another set of points
{qj}j=1k, q
j 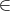 S1, called observation set, we define the corresponding to f set of
covariances
S1, called observation set, we define the corresponding to f set of
covariances
Let f be a discrete distribution on the unit circle, defined on a domain
ℙ = {pi}i=1k, p
i 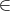 S1, thus f = {f
i}i=1k for f
i = f(pi) On another set of points
{qj}j=1k, q
j
S1, thus f = {f
i}i=1k for f
i = f(pi) On another set of points
{qj}j=1k, q
j 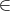 S1, called observation set, we define the corresponding to f set of
covariances
S1, called observation set, we define the corresponding to f set of
covariances
 = k (qjpi)(qjpi) f (pi).
i=1](interpol_s10x.png)
We consider two discrete distributions f1 and f2 on the unit circle, defined on the domain ℙ with corresponding set of covariances
, s = 1,2.](interpol_s11x.png)
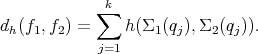
Next, we propose an interpolation criterion based on the pseudo-distance dh.
For a α 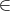 [0, 1], define
[0, 1], define
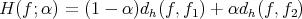
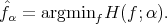
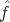 α is continuous in α at all points where H(f; α) has a well
separated minimum.
α is continuous in α at all points where H(f; α) has a well
separated minimum.
Similarity invariants h for which H(f; α) is convex functional is of particular interest for they can be easily optimized and for which the interpolation problem has a unique solution. For example, the invariant
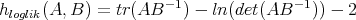
The following applet implements the proposed interpolation method for hloglik.
The solution fα is found by gradient descent algortithm. The user can specify the
number of iterations and gradient update step size. We report the minimum value
achieved H(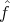 ,α) as well as the convergence curve of the gradient descent for
diagnostic. When the optimal solution is achieved, this curve is decreasing and
smoothly converges to the horizontal. Otherwise one may want to adjust the step
size and the number of iterations.
,α) as well as the convergence curve of the gradient descent for
diagnostic. When the optimal solution is achieved, this curve is decreasing and
smoothly converges to the horizontal. Otherwise one may want to adjust the step
size and the number of iterations.
What we show are the initial two distributions f1 and f2 in blue and red, the
linear interpolation (1 - α)f1 + αf2 in gray and our solution 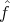 α in green. The
inner circle shows the distributions domain of size k that is uniform on S1 and the
observation points qj as black dots.
α in green. The
inner circle shows the distributions domain of size k that is uniform on S1 and the
observation points qj as black dots.