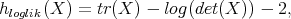
Here we implement interpolation of probability mass functions (pmf) on the unit 2-sphere. The underlying theory is exposed here.
The user may choose a family of distributions, Normal or Fisher-von-Mises, sample size, k, and similarity invariant. Three choices for invariant are available
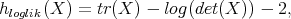
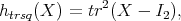
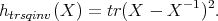
The optimization problem we try to solve is the following. For a given α in[0, 1], distribution support set {pi}i=1k and observation set {q j}j=1k, find
![∑k
ˆfh = argminf {(1 - α)γh (G Σ [f ],G Σ1 )|qj + αγh(G Σ [f ],G Σ2)|qj},
j=1](interpol_s23x.png)
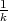 ∑
i=1k(
∑
i=1k(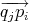 )(
)(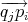 )T f
s(pi), s = 1, 2.
)T f
s(pi), s = 1, 2.
The optimization is based on gradient discent and three parameters need to be
specified, the number of iterations, gradient step size and γ. We report the
convergence curve, which serves as an indicator for the success of the descent, and
the values of H(f; α) for the linear combination 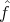 lin of f1 and f2 and the found
lin of f1 and f2 and the found
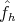 .
.
In the display window the user sees, from top left to botton right, f1, f2, flin
and 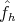 .
By dragging on the display area, one can simultaneously rotate the four spheres and visually compare the results.
.
By dragging on the display area, one can simultaneously rotate the four spheres and visually compare the results.